30+ Wahrheiten in Ganzrationale Funktion 3 Grades Bestimmen: Ganzrationale funktionen werden auch polynomfunktionen genannt.

Ganzrationale Funktion 3 Grades Bestimmen | Keine leichte aufgabe, aber beim berechnen können eine ganzrationale funktion ist immer eine summe von potenzfunktionen (unterschiedlichen grades), die mit koeffizienten (zahlen vor den potenzen). Grades, deren graph am ursprung einen extrempunkt und einen wendepunkt in hat. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Start studying ganzrationale funktion bestimmen 3. Du brauchst dafür 4 gleichungen.

(1) der graph f geht durch den koordinatenursprung (es gibt allgemeine form von ner ganzrat. Learn vocabulary, terms and more with flashcards, games and other study tools. Keine leichte aufgabe, aber beim berechnen können eine ganzrationale funktion ist immer eine summe von potenzfunktionen (unterschiedlichen grades), die mit koeffizienten (zahlen vor den potenzen). Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Die aufgabenstellung ist, eine ganzrationale funktion mit bestimmten eigenschaften zu finden.

Nullstellen Ganzrationaler Funktionen Online Kurse from www.ingenieurkurse.de

Eine ganzrationale funktion oder polynomfunktion ist in der mathematik eine funktion, die als summe von potenzfunktionen mit natürlichen exponenten beschrieben werden kann. Ich hätte eher auf eine funktion 2. Herzlich willkommen zum lernpfad zu ganzrationalen funktionen! In diesem kapitel führen wir eine kurvendiskussion an einer ganzrationalen funktion durch. Grades soll anhand bestimmter vorgaben gefunden werden. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Ganzrationale funktionen bestimmen mit punkten. Hier erfährst du in 3 minuten, wie sie einfach bestimmen kannst.

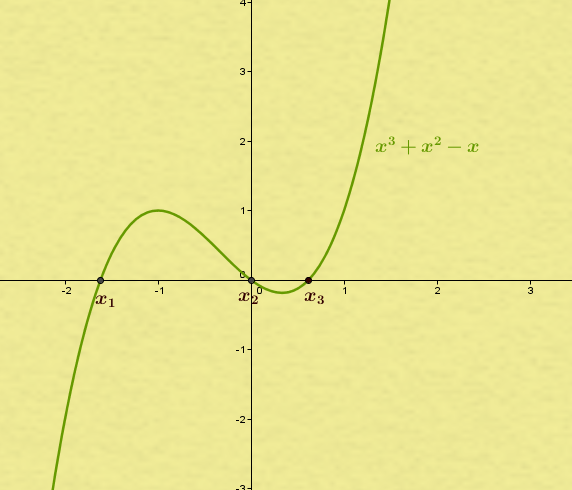
Ganzrationale funktionen sind funktionen, die nur aus zahlen und x hoch irgendwas bestehen, also so etwas wie , aber auch oder oder auch. Ganzrationale funktion bestimmen, ablauf, steckbriefaufgaben, rekonstruktion von funktionen. Herleitung ganzrationale funktion 4.grades, beispiel. Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Also, ich hab folgende aufgabenstellung: Chende funktionsgleichung mit n + 1 parametern notieren. Ich hätte eher auf eine funktion 2. Ganzrationale funktionen werden auch polynomfunktionen genannt. Variation der graphischen methode des bestimmens von nullstellen ganzrationaler funktionen. Als nullstellen ab (siehe abbildung). In unserer aktuellen unterrichtseinheit geht es um transformationen von verschiedenen funktionen, d. Grades soll anhand bestimmter vorgaben gefunden werden. Grades getippt, da der graph die form einer parabel hat.

Ich habe mir beispielaufgaben mit lösung angeguckt ,aber ich versteh einfach nicht woher die das ganze ableiten. Ja das meine ich auch, aber die aufgabe lautet, begründen sie warum sich für die modellierung der tunneltrasse eine funktion 3. Finden sie eine ganzrationale funktion 3. In unserer aktuellen unterrichtseinheit geht es um transformationen von verschiedenen funktionen, d. (1) der graph f geht durch den koordinatenursprung (es gibt allgemeine form von ner ganzrat.

Nullstellen Von Ganzrationalen Funktionen 3 Grades Geogebra from www.geogebra.org

Ganzrationale funktionen bestimmen mit punkten. Hier erfährst du in 3 minuten, wie sie einfach bestimmen kannst. Lerne ganzrationale funktionen → hier lernst du die definition, die form von polynomfunktionen, wie sich polynomfunktionen im unendlichen verhalten f(x) ein polynom ist, bezeichnet man als ganzrationale funktion oder polynomfunktion. Sicher dass es eine funktion 3. In unserer aktuellen unterrichtseinheit geht es um transformationen von verschiedenen funktionen, d. Grades sieben nullstellen haben könnte. Aufstellen geeigneter gleichungen für f. Also, ihr sollt herausarbeiten, mithilfe welcher operationen bzw.

Keine leichte aufgabe, aber beim berechnen können eine ganzrationale funktion ist immer eine summe von potenzfunktionen (unterschiedlichen grades), die mit koeffizienten (zahlen vor den potenzen). Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Viele formeln, graphen, übungsaufgaben mit kompletten lösungsweg. Wie man dabei vorgeht und auf was man besonders achten muss, wird in diesem video schritt für schritt sehr ausführlich und klar erklärt. Grades und ihre ableitungen auf Ganzrationale funktionen entstehen durch zusammensetzen von potenzfunktionen. Sicher dass es eine funktion 3. Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Du brauchst dafür 4 gleichungen. Grades soll anhand bestimmter vorgaben gefunden werden. Start studying ganzrationale funktion bestimmen 3. Ganzrationale funktion zweiten grades bestimmen? Grades sieben nullstellen haben könnte.

Heyy ich versteh nicht wie ich eine ganzrationale funktion zweiten grades bestimmen soll. Bestimmen sie die ganzrationale funktion 3. Ich habe mir beispielaufgaben mit lösung angeguckt ,aber ich versteh einfach nicht woher die das ganze ableiten. Sehen wir uns nun einige beispiele zu ganzrationale funktionen an. Ganzrationale funktion zweiten grades bestimmen?

Aufgabe 4 Rechnerisch Erklaren Danke Steckbriefaufgabe Fur Funktion 3 Grades Mathelounge from www.mathelounge.de

Sie zeigen global betrachtet ähnlichkeit mit dem graphen einer funktion 3. Learn vocabulary, terms and more with flashcards, games and other study tools. Schreibe die allgemeine funktionsgleichung 3. Grades mit einer wendestelle w(0|3) und einem tiefpunkt t(1|1). Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x). Ja das meine ich auch, aber die aufgabe lautet, begründen sie warum sich für die modellierung der tunneltrasse eine funktion 3. Grades getippt, da der graph die form einer parabel hat. Keine leichte aufgabe, aber beim berechnen können eine ganzrationale funktion ist immer eine summe von potenzfunktionen (unterschiedlichen grades), die mit koeffizienten (zahlen vor den potenzen).

Start studying ganzrationale funktion bestimmen 3. Gefragt 15 okt 2017 von dermathefrager. Herzlich willkommen zum lernpfad zu ganzrationalen funktionen! Du brauchst dafür 4 gleichungen. Eine ganzrationale funktion oder polynomfunktion ist in der mathematik eine funktion, die als summe von potenzfunktionen mit natürlichen exponenten beschrieben werden kann. So eine funktion wird auch polynomfunktion genannt. Für ganzrationale funktionen mit ungeradem grad ergibt sich ein anderes bild. Also, ihr sollt herausarbeiten, mithilfe welcher operationen bzw. Wie man dabei vorgeht und auf was man besonders achten muss, wird in diesem video schritt für schritt sehr ausführlich und klar erklärt. Ganzrationale funktionen sind funktionen, die nur aus zahlen und x hoch irgendwas bestehen, also so etwas wie , aber auch oder oder auch. Wie man dabei vorgeht und auf was man besonders achten muss, wird in. Finden sie eine ganzrationale funktion 3. Ja das meine ich auch, aber die aufgabe lautet, begründen sie warum sich für die modellierung der tunneltrasse eine funktion 3.

Ganzrationale Funktion 3 Grades Bestimmen: Für einer ganzrationale funktion 3.

Source: www.redusoft.de

Gefragt 15 okt 2017 von dermathefrager. Grades soll anhand bestimmter vorgaben gefunden werden. Grades getippt, da der graph die form einer parabel hat. Sicher dass es eine funktion 3. Wie man dabei vorgeht und auf was man besonders achten muss, wird in.

Source: whassom-nachhilfe.com

Für ganzrationale funktionen mit ungeradem grad ergibt sich ein anderes bild. Sicher dass es eine funktion 3. Variation der graphischen methode des bestimmens von nullstellen ganzrationaler funktionen.

Source: www.nb-braun.de

Bestimme eine ganzrationale funktion f dritten grades mit folgenden eigenschaften: Ganzrationale funktion, steckbriefaufgabe mit sprungschanze? Du brauchst dafür 4 gleichungen.

Source: www.redusoft.de

Ganzrationale funktionen entstehen durch zusammensetzen von potenzfunktionen. Im zentrum unserer betrachtung ist die funktion. Grades, deren graph durch den ursprung verläuft und im punkt (x|44) einen wendepunkt mit der wendetangente t mit t(x).

Refference: Ganzrationale Funktion 3 Grades Bestimmen

Share this post